주파수 응답의 그래프 표현
1. 주파수응답은 주파수에 따라 변화하므로, 서로 다른 주파수의 정현파는 다르게 작용함.
2. b_k 를 적절하게 선택하면 매우 다양한 주파수 응답을 구현할 수 있다.
주파수에 대한 주파수응답[H(e^jŵ)] 의 magnitude& phase 그래프
1. delay system
2. first-difference system
3. simple lowpass filter
+ 4. L-point running sum/average filter
1. delay system

difference equation
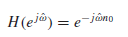
frequency response

: magnitude >> 모든 주파수에 대해 magnitude는 1이다.
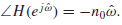
: phase

2. first-difference system
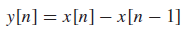

; frequency response
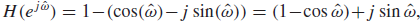
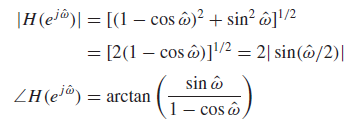
; magnitude
; phase
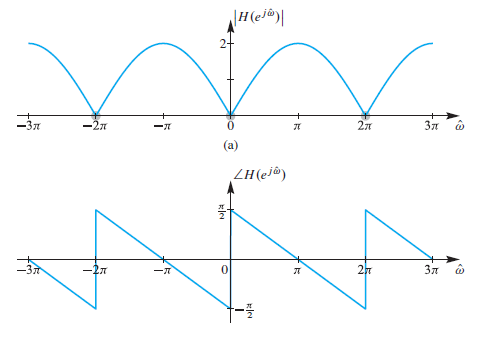
주기가 2π임을 확인할 수 있다. ( magnitude는 우함수, phase는 기함수)
magnitude의 -π 부터 π구간을 살펴보았을 때, 저주파수에서는 0, 고주파에서 2로, High pass filter 임을 알 수 있다.
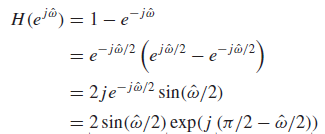
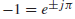
>>> j=e^(jπ /2) ,

3. simple low pass filter
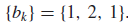
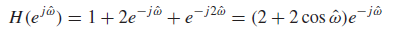
;frequency response
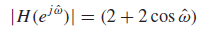

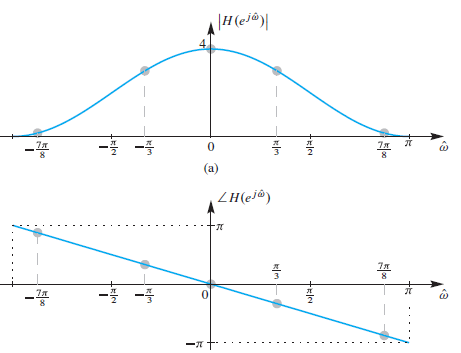
phase 가 선형형태 >> delay 발생
고주파를 억제하고, 저주파에서 magnitude가 크게 나타나므로 low pass filter이다.
Cascaded LTI system 시스템의 직렬 연결

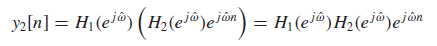

시간 영역의 convolution은 주파수영역의 multiplication과 동등하다!
Running-sum Filtering 이동합 필터링
- L-point running sum
n에서의 출력은 x[n]과 그 이전의 L-1개의 입력들의 합으로 계산된다.

; difference equation

매트랩 구현 코드:
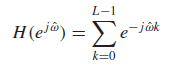
; frequency response
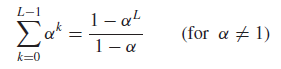
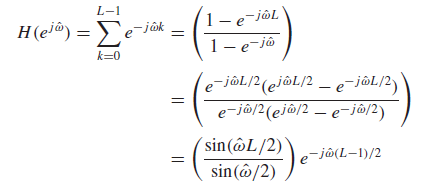
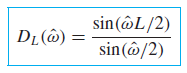
Dirichlet form(디리클레 형)
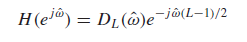
Example ) 11point running-sum filter
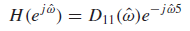
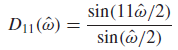
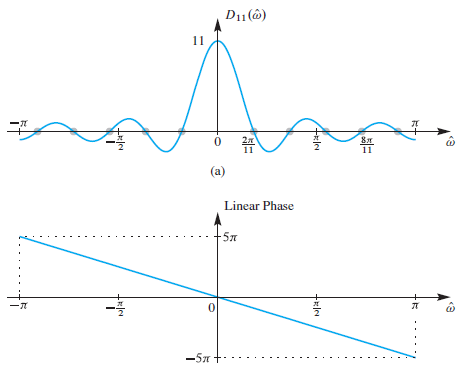
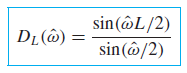
의 특징
1. 주기가 2π 인 우함수
2. ŵ가 0일 때, 최댓값 L을 가짐.
3. ŵ가 증가할수록 감소함.
4. 2π/L X k 에서 0이다. (k는 0이 아닌 정수)

phase
modulo 2π로 빼서 θ가 -π와 π 사이에 위치하도록 해준다.
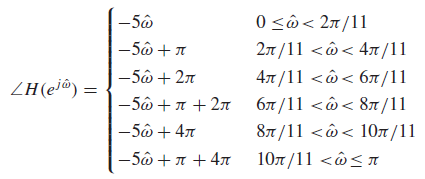
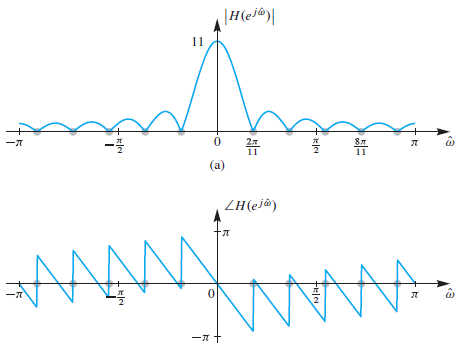
Cascaded system
1) L-point running sum 이동합
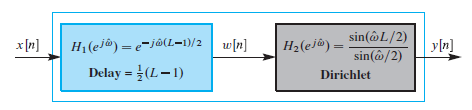
L-point running sum 이동합
(L-1)/2 만큼의 시간 delay 발생. (L=11 인 경우, -5의 shift가 발생한다.)
지연기 delay와 디리클레 필터의 직렬연결
2) L-point running-average filter 이동평균필터

L-point running-average filter 이동평균필터
이동합과 곱셈기의 직렬연결
샘플링된 연속시간 신호(Sampled Continuous-Time Signals)의 필터링
연속시간 신호를 샘플링하여 신호를 얻었을 때, 이산신호 필터의 주파수 응답을 원래의 연속시간신호의 스펙트럼에 미치는 필텨의 영향
[샘플링 / 복원]
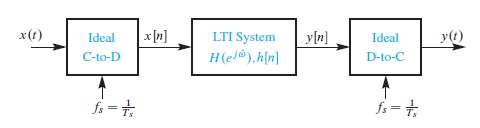

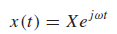
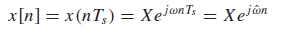
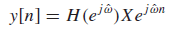
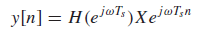
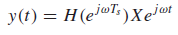
Example)
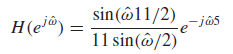
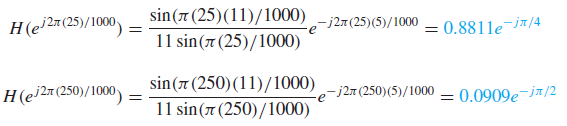
댓글